Как известно, основополагающим условием применения для оценки стоимости бизнеса метода продаж (сделок) является поиск наиболее под-ходящего предприятия-аналога, которое было продано раньше на рынке.

Применение в рамках сравнительного (рыночного) подхода метода предприятий-аналогов представляется исключительно актуальным по сле-дующим соображениям. В отечественных условиях имеют место значи-тельные колебания курса акций (голубых фишек) ведущих компаний (по акциям РАО ЕС в 2001 2002 годах наблюдалось двойное и тройное разли-чие курсовых стоимостей), сравнительно небольшой срок обращения этих акций на фондовой бирже, а также высокая вероятность манипулирования рыночной стоимостью акций крупными держателями пакетов, что является следствием недостаточной защиты прав мелких акционеров в российском законодательстве.

Подбор предприятия-аналога должен осуществляться по двум груп-пам факторов (показателей). Первая группа факторов общего плана долж-на соблюдаться в первую очередь на этапе проведения такого анализа. Вторая группа показателей предприятий одной и той же отрасли относится к категории финансово-экономических.

Их соблюдение необходимо после того, как найдены предприятия-аналоги, удовлетворяющие первой группе факторов.

В составе первой группы ключевых факторов (признаков) могут фи-гурировать следующие:

• сходство производимой продукции в рамках одноименной отрасли;
• соответствие объема и качества выпускаемой продукции;
• идентичность рассматриваемых периодов;
• тождество стадий развития предприятий (рост, зрелость, упадок);
• примерное равенство производственных мощностей;
• сопоставимость используемых стратегий развития предприятий;
• сопоставимость экономических и финансовых показателей дея-тельности предприятий;
• сходство климатических условий и территориальных расположе-ний предприятий.

Состав ключевых показателей (факторов) второй группы характери-зуется достаточно большим многообразием. К примеру, в составе этой группы могут присутствовать следующие показатели (ключевые факторы стоимости бизнеса):

• объем валовой прибыли;
• объем чистой прибыли;
• объем чистой прибыли, приходящийся на обыкновенную акцию;
• объем реализуемых услуг;
• совокупные текущие затраты;
• уровень уплачиваемых дивидендов на акцию;
• объем привлекаемых инвестиций;
• доля завоеванного рынка и др.

Перечисленными выше показателями все их многообразие не исчерпывается. В каждом конкретном случае состав показателей второй группы устанавливается экспертом-оценщиком самостоятельно.

Известно, что проданные на рынке компании практически всегда достаточно существенно различаются между собой по ключевым парамет-рам стоимости бизнеса. Найти абсолютно одинаковых проданных компа-ний не представляется возможным.

В таком случае для получения обоснованной стоимости предприятия, выставляемого на продажу, и оцениваемого с помощью метода сде-лок (продаж) принципиальное значение имеет поиск такого ранее продан-ного на рынке предприятия-аналога, ключевые параметры которого в наи-большей мере соответствовали бы первому.

Для решения этой задачи предлагается использовать многоцелевой подход, который предлагается реализовать с помощью метода анализа ие-рархий (МАИ).

Метод анализа иерархий (МАИ), разработанный Т. Саати, позволяет решать практические задачи многокритериальной оптимизации с любым количеством критериев оптимальности ¹. Целесообразность его практиче-ского использования обусловлена наличием достаточно большого количе-ства преимуществ:

1. он совмещает в себе достоинства аналитических и экспертных методов;
2. обеспечивает реализацию наиболее эффективного способа оценки количественно неизмеримых, но вместе с тем важных факторов для приня-тия обоснованных решений;
3. не предусматривает введения ограничения на транзитивность (метод работает с несогласованными суждениями и не требует, чтобы пред-почтения потребителей или ЛПР соответствовали аксиомам полезности);
4. позволяет сводить исследования сложных проблем к достаточно простой процедуре проведения последовательно попарных сравнений;
5. не предполагает прямого определения коэффициентов важности (весомостей) по показателям, используемым для оценки качества решения задачи;
6. сравнительно прост в реализации, а также не требует больших финансовых и временных ресурсов на проведение необходимых расчетов;
7. позволяет решать задачи с неограниченным количеством критериев.

Практическая иллюстрация к выбору типичного предприятия-аналога из числа ранее проданных на рынке по методу анализа иерархий

Проиллюстрируем на практическом примере последовательность расчетов по многокритериальному методу анализа иерархий (МАИ).

Допустим, что получены три варианта компаний мобильной связи, проданных на рынке. Их особенностью является то, что акционерам не вы-плачивались дивиденды.

1. Поставим перед собой цель выбрать типичный вариант предпри-ятия аналога.
2. Определимся с составом критериев (параметров), которым должен удовлетворять наилучший вариант предприятия-аналога (на рис. 1 они представлены под номерами 1 6). Как видим, задача выбора типичного предприятия-аналога является многокритериальной.
3. Представим данную проблему в виде иерархии (рис. 1).

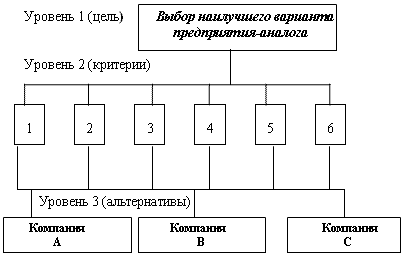
Рис. 1. Декомпозиции задачи, связанной с выбором из трех проданных на рынке предприятий типичного предприятия-аналога

Принятые обозначения критериев (параметров сравнения) на приведенном выше рисунке:

1. Объем валовой прибыли.
2. Объем реализуемых услуг.
3. Совокупные текущие затраты.
4. Объем чистой прибыли на одну обыкновенную акцию.
5. Объем привлекаемых инвестиций.
6. Доля завоеванного рынка.

Приведем краткую характеристику вариантов проданных на рынке компаний-аналогов ².

Альтернатива компания А. Компании А соответствует сравнительно небольшой объем реализуемых услуг, имеет место близкие к сред-неотраслевым текущие затраты, ниже среднего объем чистой прибыли, приходящийся на одну обыкновенную акцию, достаточно значительный объем привлекаемых инвестиций, сравнительно небольшая доля завое-ванного целевого рынка, сравнительно невысокий объем получаемой вало-вой прибыли.

Альтернатива компания В. Она выступает на рынке сотовой связи под торговой маркой "В". Компании В отвечает высокая по объему прибыль, достаточно большой объем реализуемых услуг, не ниже среднего объем чистой прибыли на одну обыкновенную акцию, вполне приемлемый объем привлекаемых инвестиций, доля занимаемого рынка оценивается как средняя, совокупная текущие затраты достаточно большие.

Альтернатива компания С. Компании С соответствует достаточно высокая валовая прибыль, сравнительно низкие текущие затраты, дос-таточно большой объем чистой прибыли, приходящийся на одну обыкно-венную акцию, достаточно большой объем привлекаемых инвестиций, сравнительно высокая доля завоеванного целевого рынка (второе место после компании В).

Для проведения субъективных парных сравнений автором метода МАИ разработана наиболее подходящая для общего случая шкала ³. Она исходит из необходимости применения соответствующих вербально-числовых оценок. Содержание этой шкалы приведено в табл. 1.

Таблица 1
Шкала относительной важности сравниваемых элементов

Интенсивность относительной важности	Определение	Объяснения
1	Равная важность	Равный вклад двух видов деятельности в цель
3	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одному виду деятельности над другим
5	Существенное или сильное превосходство	Опыт и суждения дают сильное превосходство, что оно становится практически значительным
9	Очень сильное превосходство	Очевидность одного вида деятельности над другим подтверждается наиболее сильно
2, 4, 6, 8	Промежуточные решения между двумя суждениями	Применяются в компромиссном случае
Обратные величины приведенных выше чисел	Если при сравнении одного вида деятельности с другим получено одно из вышеуказанных чисел (например, 3), то при сравнении второго вида деятельности с первым получим обратную величину (т.е. 1/3)	-

Эффективность использования приведенной выше шкалы доказана как теоретически, так и большим практическим опытом ее применения при решении многокритериальных задач в различных сферах бизнеса.

На основании изложенной выше вербальной информации и шкалы относительно важности сравниваемых критериев (параметров) заполним числовыми характеристиками матрицу попарных сравнений для уровня 2 (табл. 2).

Таблица 2
Выбор наилучшего варианта предприятия-аналога: матрица попарных сравнений для уровня 2

Параметры	1	2	3	4	5	6
1	1	2	3	5	4	2
2	1/2	1	4	7	8	1/2
3	1/3	1/4	1	7	5	3
4	1/5	1/7	1/7	1	4	1/8
5	1/4	1/8	1/5	1/4	1	1/6
6	1/2	2	1/3	8	6	1

Синтез приоритетов. На этом этапе ЛПР представил задачу в виде иерархической структуры, составил матрицу и выразил количественно субъективные парные суждения. Все приведенные в матрицах цифры оз-начают нечто конкретное. На их основе надо выбрать наилучший вариант предприятия-аналога, у которого числовые оценки исследуемых критериев представлены наиболее полно.

Ниже описывается, каким образом сочетаются иерархическая деком-позиция и шкала относительной важности для получения осмысленных подходов к многокритериальной проблеме выбора наилучшего (наиболее типичного) предприятия-аналога. Это обеспечивается посредством осуще-ствления процедуры синтеза локальных приоритетов.

Синтез: локальные приоритеты. Из группы матриц парных срав-нений формируем набор локальных приоритетов, которые выражают отно-сительное влияние множества элементов на элемент примыкающего свер-ху уровня. Находим относительную величину, ценность или вероятность каждого отдельного объекта через "решение" матриц, каждая из которых обладает обратно симметричными свойствами. Для этого нужно вычис-лить множество собственных векторов для каждой матрицы, а затем нор-мализовать (привести к безразмерному виду) результат, получая тем са-мым вектор приоритетов.

Вычисление собственных векторов это сложная задача. Одним из наилучших способов является определение геометрической средней. Это можно сделать, перемножая элементы в каждой строке и извлекая корни n-й степени, где n число элементов. Полученный таким образом столбец чисел нормализуется путем деления каждого числа на сумму всех чисел. Другой способ заключается в нормализации элементов каждого столбца матрицы и затем в усреднении каждой строки. Таким образом, можно оп-ределить не только порядок приоритетов каждого отдельного элемента, но и величину его приоритета.

После того, как компоненты собственного вектора получены для всех n строк, становится возможным их использование для дальнейших вычислений.

Следующий этап вычислений связан с нормализацией с целью получение соответствующих оценок вектора приоритетов.

На последующем этапе предусмотрена проверка уровня согласован-ности локальных приоритетов.

Согласованность локальных приоритетов. Важным элементом расчетов по МАИ является определение так называемого индекса согласо-ванности (ИС). Он дает информацию о степени нарушения численной (кардинально) и транзитивной (порядковой) согласованности.

Индекс согласованности в каждой матрице и для всей иерархии мо-жет быть приближенно получен вычислениями вручную.

Порядок его определения заключается в следующем. Сначала прово-дится суммирование элементов по каждому столбцу, затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца на вторую компоненту и т.д. Полученные числа суммируются. Таким образом, можно получить ве-личину, которую обозначим как Lmax.

Формула индекса согласованности (ИС) выглядит так;

ИС =(Lmax - n)/(n - 1),

где n - количество сравниваемых элементов (оно равно числу критериев оптимальности) .

Далее сравним каждую полученную величину с той, которая полу-чилась бы при случайном выборе количественных суждений из шкалы 1/9; 1/8; 1/7,..., 1; 2,..., 9, но при образовании обратно симметричной матрицы. Автором МАИ рекомендуются следующие средние согласованности для случайных матриц разного порядка (т.е. n):

Размер матрицы	1	2	3	4	5	6	7	8	9	10
Случайная согласован-ность	0	0	0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49

Если разделить ИС на число, соответствующее случайной согласо-ванности матрицы того же порядка, получим отношение согласованности (ОС). Величина ОС не должна быть более 20%. Если ОС выходит за эти пределы, то ЛПР нужно заново исследовать содержательную ее сторону и соответствующие количественные оценки элементов и внести необходи-мые изменения в исходные данные.

Принцип синтеза. Приоритеты синтезируются, начиная со второго уровня в направлении вниз. Локальные приоритеты перемножаются на приоритет соответствующего критерия на вышестоящем уровне и сумми-руются по каждому элементу в соответствии с критериями, на которые воздействует этот элемент. Каждый элемент второго уровня умножается на единицу, т.е. на вес единственной цели самого верхнего уровня. Это дает составной или глобальный приоритет того элемента, который затем ис-пользуется для взвешивания локальных приоритетов элементов, сравни-ваемых по отношению к нему как к критерию и расположенных уровнем ниже. Процедура продолжается до самого нижнего уровня.

Практическая иллюстрация декомпозиции, сравнительных су-ждений и синтеза. Для иллюстрации изложенных выше идей вернемся к ЛПР, который должен из трех альтернативных предприятий выбрать ти-пичное предприятие, в котором числовые оценки по исследуемым крите-риям (параметрам) представлены наиболее полно.

В табл. 3 представлена еще раз матрица парных сравнений для вто-рого уровня иерархии, которая содержит шесть критериев, воздействую-щих на общую цель.

Вычислим на данном этапе расчетов вектор приоритетов, собствен-ное значение Lmax, индекс согласованности и отношение согласованно-сти. Рассчитанные числовые данные отражены в соответствующем столбце табл. 3.

Таблица 3
Выбор наилучшего варианта предприятия-аналога: матрица попар-ных сравнений для уровня 2

Пара- метры	1	2	3	4	5	6	Произве-дение элемен- тов строк	Вектор приорите- тов
1	1	2	3	5	4	2	240	2,492883
2	1/2	1	4	7	8	1/2	56	1,955981
3	1/3	1/4	1	7	5	3	8,6625	1,4330091
4	1/5	1/7	1/7	1	4	1/8	0,00196	0,353761
5	1/4	1/8	1/5	1/4	1	1/6	0,00027	0,254231
6	1/2	2	1/3	8	6	1	15,84	1,584744
Сумма	2,78	5,515	8,67	28,25	28	6,795	8,074691	-

Осуществим процедуру нормализации вектора приоритетов. Инфор-мация, полученная расчетным путем, отражена в табл. 4.

Таблица 4
Выбор типичного предприятия-аналога: матрица попарных сравнений для уровня 2

Критерии	1	2	3	4	5	6	Вектор приоритетов	Оценка нормализованного вектора
1	1	2	3	5	4	2	2,492883	0,309
2	1/2	1	4	7	8	1/2	1,955981	0,242
3	1/3	1/4	1	7	5	3	1,433009	0,177
4	1/5	1/7	1/7	1	4	1/8	0,353761	0,044
5	1/4	1/8	1/5	1/4	1	1/6	0,254231	0,031
6	1/2	2	1/3	8	6	1	1,584744	0,196
Сумма	2,78	5,515	8,67	28,25	28	6,795	-	-

Определяем наибольшее значение матрицы суждений. Для этого сумму первого столбца умножаем на величину первой компоненты норма-лизованного вектора приоритетов, сумма второго столбца умножается на вторую компоненту нормализованного вектора приоритетов и т.д.

В нашем случае наибольшее собственное значение матрицы сужде-ний будет равно:

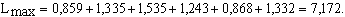
Определим численное значение индекса согласованности (ИС):

ИС = ,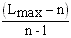

где n число сравниваемых элементов.

В нашем случае получим ИС = (7,172 - 6) : 5 = 0,234.

Определим отношение согласованности (ОС) элементов матрицы. Для этого воспользуемся средними согласованиями для случайных матриц разного порядка.

Размер матрицы	1	2	3	4	5	6	7	8	9	10
Случайная согласованность ()	0	0	0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49

В нашем случае отношение согласованности составит:

ОС = ИС : a = 0,234 : 1,24 = 0,19 (т.е. 19%).

Величина ОС не должна быть более 20%. Если ОС выходит за эти пределы, то ЛПР, решающий задачу, должен заново исследовать содержа-тельную ее сторону и соответствующие количественные оценки элементов и внести необходимые изменения в исходные данные.

В отношении матрицы попарных сравнений для уровня 3 вычислим векторы приоритетов, наибольшее собственное значение матрицы сужде-ний, индекс согласованности (ИС) и отношение согласованности (ОС).

Результаты расчетов в сводном виде приведены в табл. 5.

Таблица 5
Результаты расчетов по матрице попарных сравнений для уровня 3

Критерий 1	А	Б	В	Вектор приоритетов	Критерий 2	А	Б	В	Вектор приоритетов
А	1	1/3	1/5	0,104	А	1	1/4	1/5	0,082
Б	3	1	1/3	0,258	Б	4	1	1/7	0,184
В	5	3	1	0,638	В	5	7	1	0,733
Сумма:	9	4,33	1,53	Lmax = = 3,061	Сумма:	10	8,25	1,34	Lmax = = 3,12
				ИС=0,03					ИС=0,06
				ОС=0,05					ОС=103
Критерий 3	А	Б	В	Вектор приоритетов	Критерий 4	А	Б	В	Вектор приоритетов
А	1	1/7	1/5	0,091	А	1	1/3	1/5	0,14
Б	7	1	4	0,671	Б	3	1	4	0,585
В	5	1/4	1	0,238	В	5	1/4	1	0,275
Сумма:	13	1,39	5,5	Lmax = = 3,16	Сумма:	9	1,58	5,5	Lmax = = 3,217
				ИС=0,08					ИС=0,109
				ОС=0,14					ОС=0,879
Критерий 5	А	Б	В	Вектор приорите- тов	Критерий 6	А	Б	В	Вектор приори- тетов
А	1	1/4	1/3	1,114	А	1	1/3	1/4	0,108
Б	4	1	1/5	0,242	Б	3	1	1/5	0,211
В	3	5	1	0,644	В	4	5	1	0,679
Сумма	8	6,25	1,53	Lmax = = 3,201	Сумма	8	6,35	1,45	Lmax = = 3,187
				ИС=0,1					ИС=0,09
				ОС=0,17					ОС=0,16

Определяем численные значения глобальных приоритетов. Резуль-таты расчетов приведем в табл. 6.

Таблица 6
Результаты расчетов глобальных приоритетов

Номер критерия						Глобальный приоритет
1	2	3	4	5	6
Численное значение вектора приоритета
0,309	0,242	0,177	0,044	0,031	0,196
0,104	0,082	0,091	0,14	0,114	0,108	0,099  Альтернатива - компания А
0,258	0,184	0,671	0,585	0,242	0,211	0,319  Альтернатива - компания В
0,637	0,733	0,238	0,275	0,644	0,679	0,554 Альтернатива -компания С

Как следует из представленных в табл.3.20 результатов расчетов, типичным на рынке проданных компаний является компания МТС, так как у нее оказался наивысший глобальный приоритет (0,544).

Следовательно, рассчитанная стоимость предлагаемого для продажи на рынке любого предприятия, входящего в состав данной отрасли, должна быть откорректирована с учетом параметров, соответствующих именно те-лекоммуникационной компании С.

Сноски

1 Слияние инвестиционных компаний. Оценочный аспект // Российский клуб оценщиков http://www.appraiser.ru/info/articles/art38.htm.

2 Все примеры приведенные в илюстративном материале являются условными.

3 Слияние инвестиционных компаний. Оценочный аспект // Российский клуб оценщиков http://www.appraiser.ru/info/articles/art38.htm.