Данная статья призвана упорядочить процесс расчета стоимости акционерного капитала. В частности мы протестируем на пригодность использования в российских условиях модель американского инвестиционного банка Goldman Sachs. Основные положения этой модели уже описывались в специализированной литературе ¹, однако, в очень усеченном виде ². Выводы, сделанные на основе приложения этой модели, говорят о слабой применимости ее в российских условиях. Попробуем проверить эту модель еще раз, но только уже в полном виде.

Модель САРМ

Напомним, что с математической точки зрения стоимостью капитала является процентная ставка, используемая для пересчета будущих потоков доходов в единую величину текущей стоимости. В экономическом смысле стоимость капитала представляет собой альтернативную доходность, которую можно получить на фондовом рынке от инвестирования в бумаги, подобные по риску и сроку погашения рассматриваемому объекту инвестирования.

Существует несколько подходов к определению стоимости акционерного капитала. Наиболее часто на практике используются три модели: модель оценки долгосрочных активов (Capital Asset Pricing Model, САРМ), модель кумулятивного построения и модель мультипликатора. В данной статье основное внимание будет уделено модели оценки долгосрочных активов, в частности ее трактовке банком Goldman Sachs.

Основная идея модели оценки долгосрочных активов заключается в том, что существует только один источник риска, влияющий на долговременную доходность вложений в реальные активы и ценные бумаги. Модель САРМ утверждает, что этот риск есть рыночный риск, т.е. тенденция акций изменять свои позиции относительно уровня рынка акций в целом. В модели САРМ этот рыночный риск измеряется с помощью показателя бета.

Модель оценки долгосрочных активов имеет следующий вид:

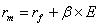или ,

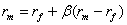где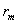 - рыночная ставка доходности;
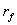- безрисковая ставка доходности;
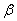- "бета"-коэффициент, для рынка в целом равный единице;
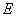- премия за риск вложения в акции, равна .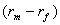

Гипотетически безрисковая ставка равна доходности ценной бумаги или портфеля ценных бумаг, ни при каких обстоятельствах не подверженных риску невыполнения обязательств, и поэтому она совершенно не коррелирует с другими доходностями в экономике. Теоретически наилучшим материалом безрисковой ставки была бы доходность инвестиционного портфеля с нулевой бетой. Но поскольку формирование таких портфелей с нулевой бетой - дело дорогостоящее и весьма сложное, этот инструмент оценки безрисковой ставки не используется.

В качестве безрисковой ставки дохода в мировой практике обычно используется ставка дохода по долгосрочным государственным долговым обязательствам (облигациям или векселям) с аналогичным исследуемому проекту горизонтом инвестирования. Например, в США обычно используется процентная ставка десятилетних казначейских облигаций. Среди причин выбора именно этой ставки выделяются следующие положения ³.

Во-первых, это долгосрочная процентная ставка, которая более других соответствует продолжительности денежных потоков оцениваемой компании. Текущая ставка казначейских векселей - ставка краткосрочная, и поэтому она не вполне соответствует продолжительности денежных потоков. Если приходится пользоваться краткосрочной ставкой, то самый приемлемый выбор в таком случае - ожидаемые краткосрочные ставки на каждый будущий период, а не сегодняшняя краткосрочная ставка. По сути, десятилетняя процентная ставка представляет собой среднее геометрическое значение ожидаемых краткосрочных ставок по казначейским векселям за весь период оценки.

Во-вторых, долгосрочная процентная ставка более устойчива с течением времени, а значит менее рискованная, чем краткосрочная. Например, Рисунок 1 иллюстрирует изменение процентных ставок в двух странах США и Новой Зеландии. При этом краткосрочная процентная ставка сильнее изменяется и в США (за шесть лет ставка упала на 77%, а долгосрочная - только на 28%) и в Новой Зеландии (почти за четыре года краткосрочная ставка упала на 74%, а долгосрочная - только на 55%).

Рисунок 1. Доходности к погашению государственных облигаций США и Новой Зеландии

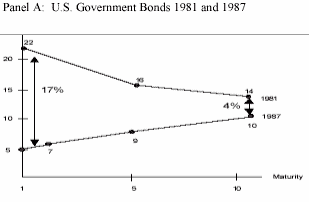
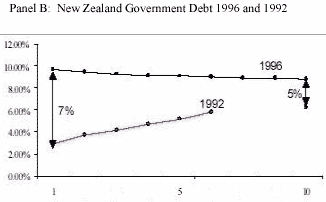
Источник: Monitor Group ⁴

В-третьих, десятилетняя ставка по своему временному горизонту близка портфелю акций рыночного индекса, и в силу этого она совместима с бетой и рыночной премией за риск, относящийся к этому рыночному портфелю.

В-четвертых, десятилетняя ставка характеризуется меньшей чувствительностью к неожиданным колебаниям инфляции, а также меньшей премией за ликвидность относительно более долгосрочных ставок.

Премия за риск вложения в акции представляет собой разницу между ожидаемой доходностью рынка и безрисковой процентной ставкой. Показатель общей доходности рынка представляет собой среднерыночный индекс доходности и рассчитывается на основе долгосрочного анализа статистических данных в соответствии с гипотезой о детерминированности или взаимосвязанности цен на акции с искомой фундаментальной стоимостью предприятий.

Обычно ⁵ используют среднее геометрическое значение доходности (Compound Annual Grow Rate, CAGR), поскольку оно более точно отражает ожидаемую инвесторами доходность за продолжительные периоды времени. По крайней мере, именно такой подход ⁶ используется в исследованиях представителей компании "Ibbotson Associates". Данные по доходности активов этой компании - Stocks, Bonds, Bills, and Inflation: Yearbook - публикуются в каждом уважаемом учебнике по корпоративным финансам.

Среднеарифметическая доходность - это просто среднее значение доходностей за единственный период, соответственно средние арифметические значения разнятся в зависимости от периода оценки. Средняя геометрическая доходность - это доходность со сложным начислением, которая уравнивает исходную и конечную стоимости.

Существуют обоснованные доводы ⁷ в пользу использования именно среднего геометрического. Во-первых, эмпирические исследования показывают, что доходность акций статистически коррелирует во времени. Иными словами, удачные годы с бoльшей вероятностью сменяются неудачными годами, и наоборот. Следовательно, среднеарифметическая доходность завышает доходность. Во-вторых, хотя модель САРМ может быть моделью с одним периодом, ее использование для получения ожидаемых доходов на длительных периодах (например, 5-10 лет) предполагает, что единичный период может значительно превышать один год.

Расчет средней геометрической доходности производится по двум равноценным формулам ⁸:

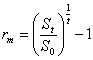или ,

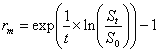где 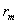- средняя геометрическая доходность;
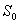- начальное значение индекса;
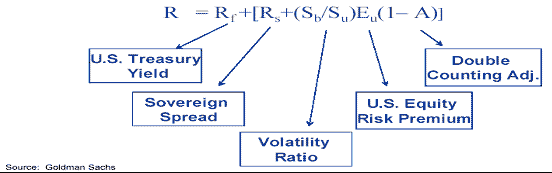
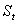- значение индекса через период времени t;
exp - экспонента (показательная функция с основанием натурального логарифма e = 2,178).

Среднегеометрическое значение рыночной премии за риск в США за период 1926-2000гг. составляло 5,24%. Долгосрочное значение премии предполагается на уровне 4% ⁹.

Модель САРМ от Goldman Sachs

Модель Goldman Sachs была специально разработана для использования в портфельном инвестировании на развивающихся рынках Латинской Америки, Азии и стран Восточной Европы. В интерпретации ¹⁰ Goldman Sachs формула модели САРМ имеет следующий вид:

где 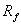- доходность государственных облигаций США;
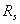- спрэд доходностей государственных облигаций США и развивающейся страны;
- изменчивость индекса фондового рынка развивающейся страны;
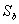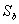- изменчивость индекса фондового рынка США;
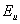- рыночная премия за риск для условий США;
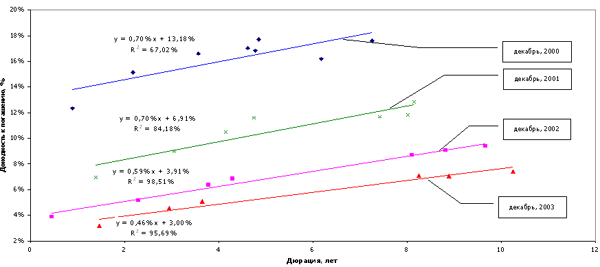
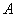- коэффициент корреляции рынков государственных облигаций и фондового рынка развивающейся страны.

В модели Goldman Sachs в качестве безрисковой ставки используется доходность 30-летних государственных облигаций США. В качестве страновой риск-премии используется спрэд доходностей государственных облигаций США и развивающейся страны. Премия за риск инвестирования в акции рассчитывается на основе рыночной премии для условий США скорректированной на отношение изменчивостей индексов развивающейся страны и США, а также на коэффициент, позволяющий исключить двойной учет рисков. Например, валютный риск учитывается и в доходности еврооблигаций, и в доходности фондового индекса.

Изменчивость индекса фондового рынка определяется как стандартное отклонение ежедневных изменений индекса за шестимесячный период. Коэффициент, позволяющий исключить двойной учет рисков, рассчитывается как разница между единицей и коэффициентом корреляции рынков государственных облигаций и фондового рынка развивающейся страны. Корреляция рынков определяется на шестимесячном отрезке времени.

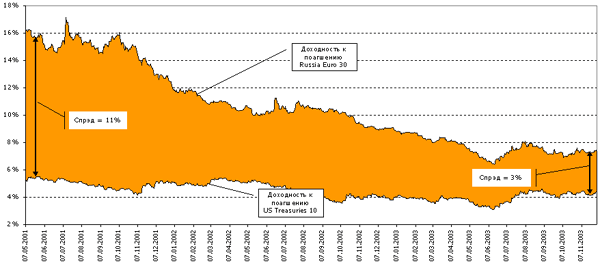
Дополнительно стоит отметить, что выше представлена модель САРМ для рынка в целом. Для расчета стоимости акционерного капитала отдельной компании в модели Goldman Sachs используется коэффициент 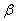. Этот коэффициент умножается на рыночную премию за риск, которая в модели представлена выражением в квадратных скобках за вычетом спрэда доходностей.

Все элементы модели Goldman Sachs обозначены, соответственно можно перейти к расчету стоимости акционерного капитала для российского рынка в целом. Расчет базируется на фактических данных, зафиксированных на 01.01.2004г.

Расчет стоимости капитала

Для расчета безрисковой ставки обратимся к российскому рынку фиксированной доходности. На рынке присутствуют государственные еврооблигации номинированные в долларах США с периодом обращения 30 лет. Однако дюрация, т.е. эффективный срок погашения, этих облигаций никогда не превышала 10-11 лет, а на момент расчета составляла около 9 лет. Соответственно и в модели Goldman Sachs следует использовать доходность американских государственных облигаций с сопоставимым сроком.

Доходность к погашению российских еврооблигаций с декабря 2000г. по декабрь 2003г. значительно снизилась. Исходя из линейных трендов кривых доходности облигаций, основное снижение пришлось на постоянную часть доходности, которая сократилась с 13,2% до 3%. При этом переменная часть сократилась немного, с 0,7% до 0,5%.

Рисунок 2. Кривые доходности суверенных еврооблигаций России

Снижение доходности еврооблигаций количественно выражает понижение страновых рисков инвестирования в экономику России относительно страновых рисков инвестирования в США. Рисунок 3 иллюстрирует снижение спрэда доходностей облигаций двух стран с 11% до 3%.

Рисунок 3. Оценка странового риска России исходя из доходностей еврооблигаций России и облигаций США

Исходя из линейных трендов кривых доходности государственных еврооблигаций на начало 2004г., безрисковая ставка доходности для временного интервала в 10 лет составляла 7,6%. Это значение ставки подразумевает 4,6% безрисковую ставку для США и 3% премию за российские страновые условия инвестирования.

Теперь рассчитаем премию за риск инвестирования в акции. Значение этой премии для условий США примем на ранее уже упоминаемом уровне долгосрочного значения 4%.

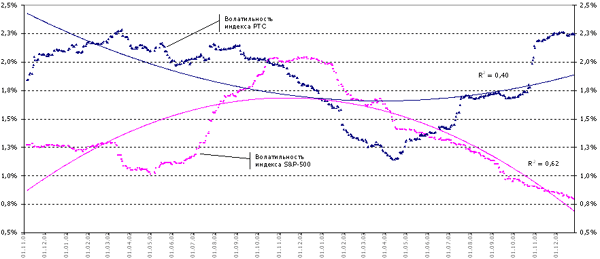
Стандартное отклонение дневной доходности индекса РТС за шесть месяцев до 01.01.2004г. составляло 2,24%. Стандартное отклонение дневной доходности индекса S&P500 за тот же временной период составляло 0,80%. Отношение первого ко второму составляло 2,82. Графически динамика шестимесячных стандартных отклонений двух индексов представлено ниже на рисунке.

Стоит отметить, что были краткосрочные периоды, когда волатильность индекса РТС была ниже волатильности индекса S&P500. Однако впоследствии все встало на свои места.

Рисунок 4. Волатильность фондовых индексов России и США

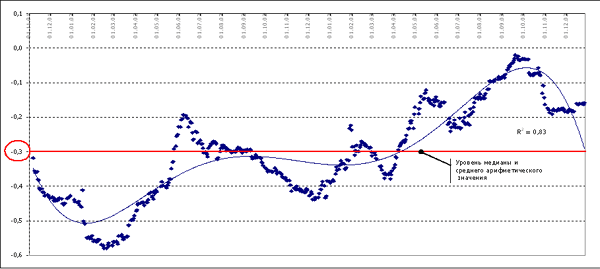
Коэффициент корреляции дневных изменений индекса РТС и изменения доходности к погашению еврооблигаций Россия-30 за шесть месяцев до 01.01.2004г. составил (-0,16). Стоит отметить, что среднее арифметическое коэффициентов корреляции составляет (-0,30), такое же значение имеет и медиана массива. Соответственно, долгосрочное значение коэффициента корреляции будет колебаться именно у отметки (-0,30), увеличивая тем самым рыночную премию.

Рисунок 5. Корреляция еврооблигаций и фондового рынка России

Подставим в модель Goldman Sachs все полученные значения:

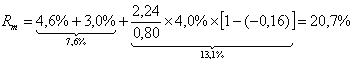
Таким образом, получается, что стоимость акционерного капитала российского фондового рынка в целом составляет 20,7%, в т.ч., безрисковая премия 7,6% и премия за риск 13,1%.

Стоит отметить, что в октябре 1999г. банк Goldman Sachs для России определял стоимость капитал на уровне 35,1%. На последующие пять лет по прогнозу банка ставка должна была составить в среднем 22,2% ¹¹.

На первый взгляд больше всего вопросов вызывает полученное значение премии за риск, так как оно представляется завышенным. И в правду сказать, отечественные и зарубежные инвестиционные банки и компании в своих расчетах ¹² по российскому рынку за последние два года использовали премию за риск на уровне 3-6%. Только один американский инвестиционный банк применял ¹³ сопоставимую с нашим результатом премию за риск - 14,4%. Поэтому целесообразно было бы проверить полученное значение премии.

Проверка модели Goldman Sachs

Проверка будет заключаться в расчете премии за риск как разности между исторической доходностью российского фондового рынка и безрисковой ставкой.

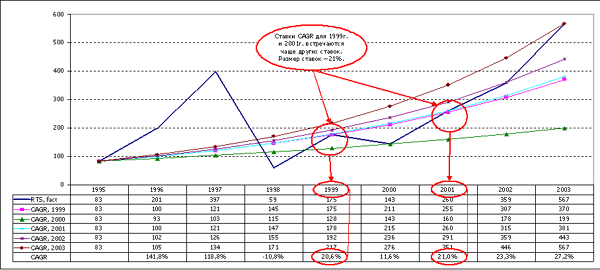
Средняя геометрическая доходность фондового рынка России по индексу РТС за период 1995-2003гг. составляла 27,2%. Внизу на графике показаны фактические значения индекса РТС, а также прогнозные значения, построенные с помощью вычисленных ежегодных среднегеометрических доходностей (CAGR). Как видно, наиболее часто пересекают линию фактических значений индекса РТС линии, построенные с помощью двух ставок доходности - 1999г. и 2001г. Значение этих ставок составляло 20,6% и 21,0% соответственно. Среднее арифметическое этих двух значений составляло 20,8%. Среднее арифметическое пяти значений ставки за период 1999-2003гг. составляло 20,7%.

Рисунок 6. Фактические значения индекса "РТС" на конец года (1995-2003гг.), а также прогнозные значения, построенные на основе среднегеометрических ставок по годам (1999-2003гг.)

Таким образом, ожидаемое на начало 2004г. значение средней геометрической доходности фондового рынка России составляет 20,8%.

Значение безрисковой ставки доходности мы уже рассчитывали, и оно составляет 7,6%.

Тогда российская премия за риск составит: 20,8% - 7,6% = 13,2%.

Полученные значения ставок премии за риск 13,1% по модели Goldman Sachs и 13,2% по стандартной модели САРМ различаются между собой совсем незначительно. Соответственно, можно считать, что модель Goldman Sachs работает в российских условиях.

На наш взгляд, различия в значениях премии за риск, используемых на практике и полученных в данной статье, можно объяснить использованием инвестиционными банками (осознанно или нет) двух методов управления рисками:

1. Компенсация рисков. Это означает, что инвестиционный банк покрывает часть рисков не за счет ставки дисконтирования, а за счет денежного потока. Обычно это делается путем сверхконсервативного прогноза цен на продукцию оцениваемых компаний, однако при этом отсутствуют возможные альтернативные сценарии изменения уровня цен.
2. Принятие риска. Это означает, что инвестиционный банк косвенно оставляет часть риска под свою ответственность. Другими словами, для того, чтобы была возможна активная торговля ценными бумагами, у последних должен быть потенциал роста, который очень часто появляется вследствие объективного или субъективного снижения их рисков, в частности уменьшения премии за риск в ставке дисконтирования.

Таким образом, полученное в данной статье с помощью модели Goldman Sachs значение премии за риск следует очень аккуратно использовать на практике, осознавая тот факт, что учесть риск можно, а иногда и нужно, иным способом.

Ссылки на литературу

1. Шипов В.Н. "Некоторые особенности оценки стоимости отечественных предприятий в условиях переходной экономики" // "Рынок Ценных Бумаг", №18, 2000г. http://www.rcb.ru/Archive/articlesrcb.asp?aid=1406
   Рекомендуется также прочитать комментарий к статье: http://www.rcb.ru/Archive/golosbook.asp?aid=1406
2. На наш взгляд неполнота приводимой в статье Шипова В.Н. модели Goldman Sachs связана с тем, что автор в качестве источника использовал не первичный материал, а вторичный. Этот вывод основывается на драфте печатной версии статьи "Учет риска через ставку дисконтирования при оценке стоимости российских предприятий в современных условиях", где в качестве источника приводится ссылка на статью в Bloomberg. Драфт статьи Шипова В.Н. можно найти здесь: http://zhurnal.ape.relarn.ru/articles/2000/074.pdf
3. Copeland T., Moel A. Comments on beta and on the risk-free rate when using the CAPM to calculate WACC. Monitor Group, July 2003; Коупленд Т., Колер Т., Мурин Дж. Стоимость компаний. Оценка и управление /Пер. с англ. - М: Олимп-Бизнес, 2000, стр.283.
4. Copeland T., Moel A. (2003)
5. Коупленд Т., Колер Т., Мурин Дж. (2000), стр.284-286.
6. Ibbotson R., Chen P. Long-Run Stock Returns: Participating in the Real Economy. Financial Analysts Journal. January/February 2003, Volume 59, Number 1.
7. Дамодаран А. Инвестиционная оценка. Инструменты и техника оценки любых активов /Пер. с англ. - М.: Альпина Бизнес Бук, 2004, стр.212.
8. Уотшем Т.Дж., Паррамоу К. Количественные методы в финансах /Пер. с англ. - М: ЮНИТИ, 1999, стр.20, формула (1.15), стр.43-44 формула (1.29).
9. Ibbotson R., Chen P. (2003).
10. Русскоязычное описание модели базируется на трех отчетах банка Goldman Sachs: Mariscal J., Hargis K. A Long-Term Perspective on Short-Term Risk, 26 October 1999; Mariscal J., Hargis K., Baird A., Chan V. Emerging markets discount rates. A consistent market-based methodology for Asia, EMEA and Latin America, 22 March 1999; Mariscal J., Lee R. The Valuation of Mexican Stocks: An Extension of the Capital Asset Pricing Model to Emerging Markets, 18 June 1993.
11. Mariscal J., Hargis K. A Long-Term Perspective on Short-Term Risk, 26 October 1999.
12. Deutsche Bank. Svyazinvest. The regulator holds the key, 10 April 2002 (премия за риск 5,5%, стр.33);
    Raiffeisen Centrobank. Norilsk Nickel. Sell on Strength, 30 May 2002 (30% от безрисковой ставки - максимальная 3,45%, минимальная - 2,85%, стр.11);
    Credit Suisse First Boston. Russian electric utilities. Beware the state of euphoria, 27 May 2003 (6%, стр.8);
    Brunswick UBS. VSMPO. The global titanium giant, 2 April 2004 (4%, стр.34);
    Тройка-Диалог. Россия в цифрах. Рынок и страновой риск, 2 июля 2002 (4%, стр.2);
    Альфа-Банк. Изменение в методе определения рекомендации по акциям, 9 июня 2003 (средняя премия 5%, для лидеров рынка - 3%, для "второго эшелона" - 9%, стр.6);
    Aton Capital Group. Вимм-Билль-Данн. Прогнозируемая цена снижена, рекомендация "Покупать" сохраняется, 15 апреля 2004 (5%, стр.14);
    Renaissance Capital. Russian Equities: Hunting For The Value, 14 May 2004 (6%, стр.7).
13. Bear Stearns. Unified Energy Systems of Russia: "Tariffic" Upside Unlikely, 11 August 2003 (премия за риск 14,4%, стр.86)